 CuaimaCrypt is a cypher designed by Julian Bolivar-Galeno in 2007, with improvements suggested by Jonathan Pastran during the development period.
CuaimaCrypt is a cypher designed by Julian Bolivar-Galeno in 2007, with improvements suggested by Jonathan Pastran during the development period.
CuaimaCrypt originally had two versions, CuaimaCrypt Stream Codec (CuaimaCrypt-SC) which was designed for hardware implementation, making encoding data streams in real time; and CuaimaCrypt Block Codec (CuaimaCrypt-BC) which was designed for software implementation because it uses the capacity of PCs to process data blocks efficiently.
Currently the most distributed and used is the CuaimaCrypt-BC and I will focus this article on it.
Traditional cryptographic algorithms such as AES, RC4, Blowfish, DES, Triple DES, Serpent, Twofish and others, have predetermined fixed structure.
CuaimaCrypt has a dynamic structure, due to this the structure is unknown in advance, only the basic layout is defined.
The CuaimaCrypt ‘s structure is determined based on the key used; this feature together with the coding blocks operation makes it more robust to cryptanalysis than traditional algorithms and current Quantum Computer attacks resistant as was exposed in my other article “NSA Believe that Current Cryptography Algorithms Are Broken by New Quantum Computers”.
The CuaimaCrypt’s heart is the Shift-Codec and Shift-Decodec who are those that allow the encoding and decoding the clear data.
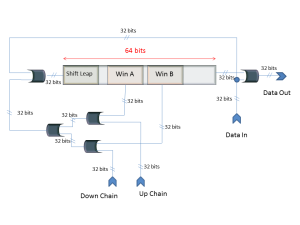
The Shift-Codec, consists of a 64-bit shift register, five 32 bits XOR gates; also it has two internal 32-bit windows (Win A and B) and a “Shift Leap” parameter which determines how many bits are going to be shifted by the register at each iteration; another important point is, the Shift-Codec have a “Up Chain and “Down Chain”, which are linked to other Shift-Codec in CuaimaCrypt’s structure, also in the shift register are defined two anchor points “Up Chain” and “Down Chain” from other two Shift-Codec in CuaimaCrypt.

The Shift-Decodec, has an identical structure to the Shift-Codec, the difference between the Shift-Decodec and the Shift-Codec is the feedback point for the upper loop which uses the clear data to feedback the loop; this is very important for the system security due to two reasons, the first is that in order to decode data at time t+(64/”shift leap”) must have successfully decoded the data at time t, otherwise the outcome data will be useless because the system will diverged from the original sequence. The second is with this feedback the shift register does not suffer from the drawbacks of linear feedback shift registers (FSR), which the problems of sub-cycles or shorter cycles. Due to the feedbacks loop, the “up and down chain” connections, the “shift-leap” and the dependence of the clear data, the Shift-Codec and Shift-Decodec not have cycles that can be predicted by cryptanalysis.
The Shift-Codes and Shift-Decoder form a mesh using the “Up Chain” and the “Down Chain”, each connection “Up Chain” and “Down Chain” are bind to a single Shift-Codec or Shift-Decodec, but not necessarily the same, and each Shift-Codec or Shift-Decodec can only receive an “Up Chain” and “Down Chain”, so the connections are unique among Shift-Codec or Shift-Decodec, additionally the connection point where is extracted the shift-register’s data is dynamic.
These connections must be initialized before start coding and must be key dependent.
The Shift-Leap is a parameter that defines how many bits are going to be shifted in each cycle, this value is between 1 bit and 15 bits per cycle.
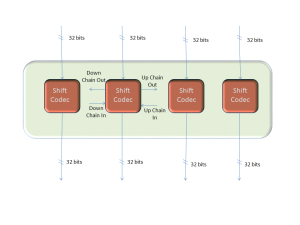
The Rake Codec and the Rake Decoder are formed by grouping four Shift Codec and four Shift Decodec respectively.
This group of Shift Codec and Shift Decoder can process blocks of 128 bits.
The byte scramblers are functions that combine the four 32-bit outputs form the Rake Codec or Rake Decodec; These are used to increase the coding’s entropy as it mixes the most significant and the least significant bytes.
The interleaving is used to make orthogonal the input data using a Walsh code in order to produce an equal distribution of 1 and 0 in the data. It makes a mixture of the most and less significant bits.

The scramblers and the interleaving help to produce a flatter distribution of values over the ASCII table.
CuaimaCrypt in its most basic form is formed by interleaving the input data, two blocks Rake Codec and one Scrambler between Rake Codec.
One of the strengths of CuaimaCrypt is that this structure could be repeated almost indefinitely, depending on available memory and encoding rate required to increase the level of security required by the application, at the present for the Valhala’s most classified documents we are using CuaimaCrypt with 512 blocks.
The CuaimaCrypt’s initialization is set using the following parameters:
- Number of blocks.
- Seeds of Shift Codec.
- Sequence of Scramblers to be used between blocks.
- Hopping sequence between Shift Codecs.
- Up Chains on each Shift Codec.
- Down Chains on each Shift Codec.
- Start Point window for each Up Chain Shift Codec.
- Start Point window for each Down Chain Shift Codec.
- Start Point window for Win A in each Shift Codec.
- Start Point window for Win B in each Shift Codec.
- Shift Leap for each Codec
- Walsh code to be used in the interleaving.
The initialization process can be performed by any method chosen by the programmer using the library, but to determine the security of the algorithm is imperative to be very careful in the way to implement it.

At the Valhala Networks’ implementation, to initialize CuaimaCrypt we are using Lorenz attractors.
The Lorenz attractor is a concept introduced by Edward Lorenz in 1963, it is a three-dimensional deterministic nonlinear dynamic system derived from simplified equations of convection rolls that occur in the dynamic equations of the atmosphere.
For certain values of the system’s parameters, it exhibits chaotic behavior and show what is now called a strange attractor.
Tucker proved in 2001, the strange attractor in this case is a fractal of Hausdorff’s dimension between 2 and 3. Grassberger (1983) estimated the Hausdorff’s dimension in 2.06 ± 0.01 and a correlation 2.05 ± 0.01.

In order to perform the CuaimaCrypt’s parameters initialization, the Lorenz attractor are used to generate a pseudorandom sequence difficult to determine without knowing precisely the starting points that was chose.
To determine the CuaimaCrypt’s security level is necessary to establish a comparative framework which should be equivalent to that used by other encryption algorithms, CuaimaCrypt’s operation is different and is necessary to determine a key length equivalence that include all the CuaimaCrypt’s initialization process.
The equation that define the possible combinations of CuaimaCrypt’s configuration is:
![]()
Where N is the number of blocks in the algorithm.
Number of Blocks N | CuaimaCrypt’s Configuration Combinations | Equivalent Key Bits Length |
2 | 3.6855×10 ^ 165 | 550 |
4 | 5.4648×10 ^324 | 1078 |
6 | 7.1220×10 ^ 484 | 1610 |
9 | 2.0384×10 ^ 726 | 2412 |
16 | 5.6466×10 ^ 1293 | 4297 |
32 | 2.0153×10 ^ 2603 | 8647 |
64 | 1.8187×10 ^ 5250 | 17440 |
128 | 8.2660×10 ^ 10600 | 35215 |
256 | 5.9661×10 ^ 21416 | 71144 |
512 | 4.2701×10 ^ 43278 | 143768 |
1024 | 4.6637×10 ^ 87463 | 290548 |
In perspective at the observable universe we have in a gross underestimation of 1×10^29 stars according to astronomers’ estimates.
If we compare these values with known symmetric key algorithms we can see:
- AES: 256 bits
- Blowfish: 448 bits
- Serpent: 256 bits
- Twofish: 256 bits
- GOST: 256 bits
- REDOC: 160 bits
- IDEA: 128 bits
- MMB: 128 bits
- SAFER K-128: 128 bits
- NewDES: 120 bits
- 3-WAY: 96 bits
- CRAB: 80 bits
- SKIPJACK: 80 bits (Clasificated algorithm by NSA)
- CAST: 64 bits
- Madryga: 64 bits
- FEAL: 64 bits
- LOKI: 64 bits
- SAFER K-64: 64 bits
- DES: 56 bits
CuaimaCrypt is a mature algorithm with 9 years in the market without any, reported or known, security fails at Valhala Networks’s implementations.

If you want to try a powerful implementation of the CuaimaCrypt algorithm for all platforms, just please visit CuaimaCrypt Command Line (ccli) at Valhala Networks’ web site.
Julian Bolivar-Galeno is an Information and Communications Technologies (ICT) Architect whose expertise is in telecommunications, security and embedded systems. He works in BolivarTech focused on decision making, leadership, management and execution of projects oriented to develop strong security algorithms, artificial intelligence (AI) research and its applicability to smart solutions at mobile and embedded technologies, always producing resilient and innovative applications.
CuaimaCrypt, a Strong Cryptographic Alternative
No comments:
Post a Comment